使用WebGL讲解3D坐标系下的点的转换矩阵
1. 平移 (Translation)
在3D空间中,假设我们需要将一个点平移到另一个位置。假设空间中的一点P,其用坐标表示为(x,y,z);将其向 x方向平移 tx,向y方向平移ty, 向z方向平移tz, 设平移后点的坐标为(x’,y’,z’),则上述点的平移操作可以归纳为如下公式:
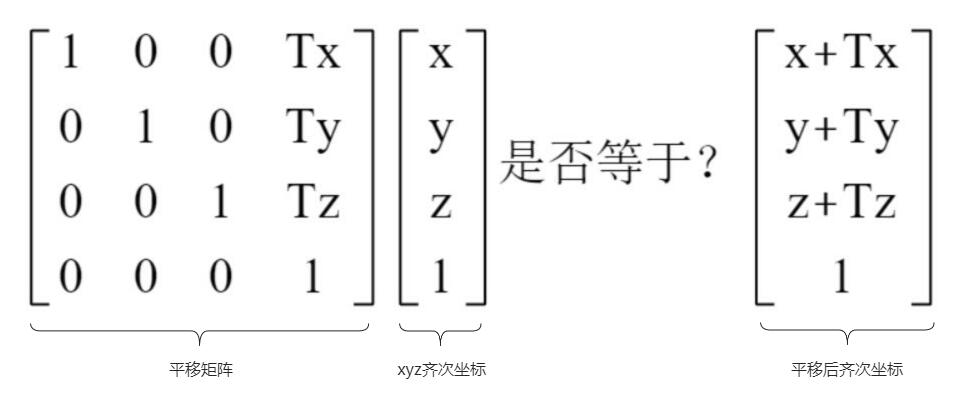
2. 缩放 (Scaling)
在3D空间中,对点(x,y,z)常用的另一种操作为相对于另一点(px,py,pz)进行缩放操作,我们不妨x方向的缩放因子为sx,y方向的缩放因子为sy,z方向的缩放因子为sz, 则上述点(x,y,z)相对于点(px,py,pz)的缩放操作可以归纳为如下公式:
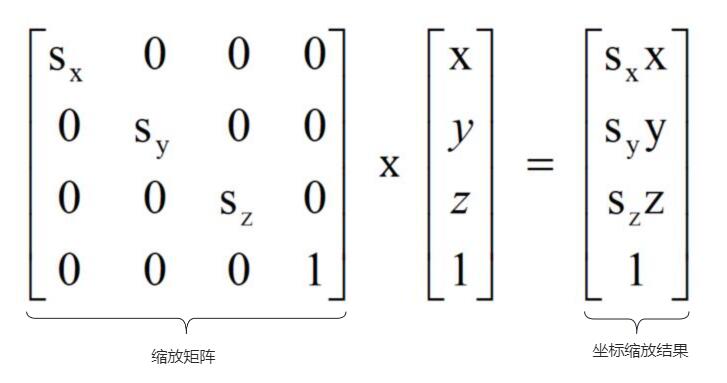
3. 旋转(Rotation)
在3D空间中,对点(x,y,z)常用的另一种操作为相对于另一点(px,py,pz)进行旋转操作,我们依旧采用右手坐标系,即旋转角的正方向为逆时针方向。旋转我们可分为绕x轴、y轴、z轴旋转。假设绕x轴旋转角度为alpha,绕y轴旋转角度为beta,绕z轴旋转的角度为gamma。则相应的变换如下:
绕Z轴旋转γ角度,z的坐标不变不变,x、y的坐标发生变化,如果你有兴趣,可以用你高中的三角函数知识推理,可以知道旋转后的坐标:
X=xcosγ-ysinγ,Y=xsinγ+ycosγ
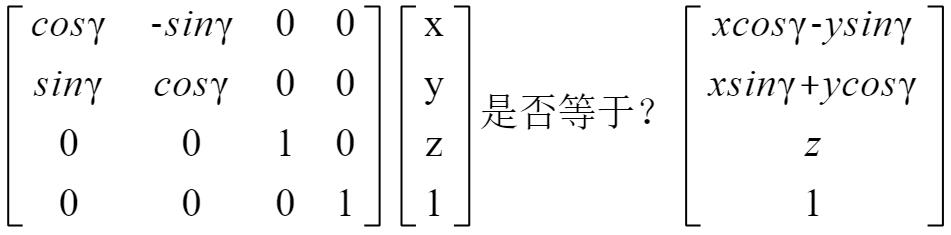
绕X轴旋转α角度
x的坐标不变,y、z的坐标发生变化,Y=ycosα-zsinα,Z=ysinα+zcos
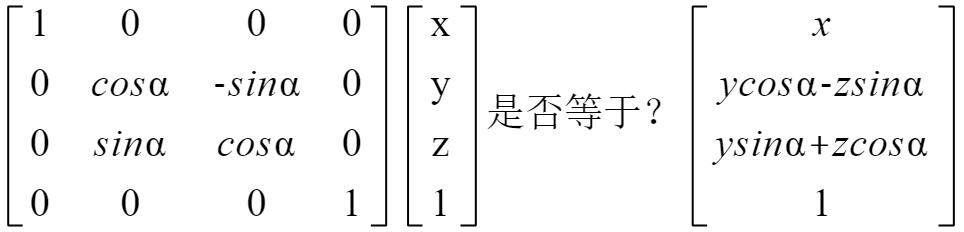
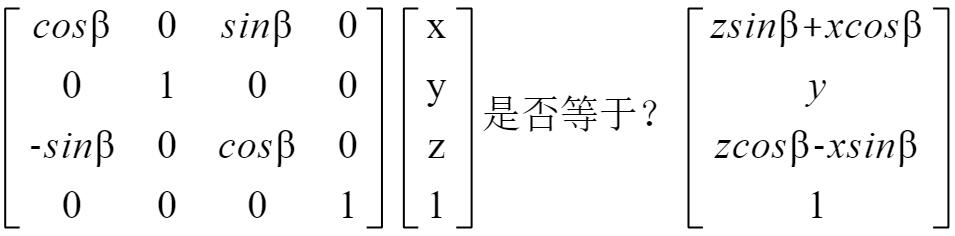
绕Y轴旋转β角度
y的坐标不变,z、x的坐标发生变化,Z=zsinβ+xcosβ,X=zcosβ-xsinβ
使用webGL代码表示
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<title>作者个人博客 liubf.com</title>
</head>
<body>
<canvas
id="webgl"
width="500"
height="500"
style="background-color: #0d72da"
></canvas>
<!-- 顶点着色器源码 -->
<script id="vertexShader" type="x-shader/x-vertex">
//attribute声明vec4类型变量apos
attribute vec4 apos;
void main() {
// 创建平移矩阵
//1 0 0 -0.4 // tx
//0 1 0 -0.4 // ty
//0 0 1 -0.4 // tz
//0 0 0 1
mat4 translation = mat4(1,0,0,0, 0,1,0,0, 0,0,1,0, -0.4,-0.4,-0.4,1);
// 缩放矩阵
// 0.5 0 0 0 // sx
// 0 0.5 0 0 // sy
// 0 0 0.5 0 // sz
// 0 0 0 1
mat4 scale = mat4(0.5,0,0,0, 0,0.5,0,0, 0,0,0.5,0, 0,0,0,1);
//设置几何体轴旋转角度为30度,并把角度值转化为弧度值
float radian = radians(30.0);
//求解旋转角度余弦值
float cos = cos(radian);
//求解旋转角度正弦值
float sin = sin(radian);
//引用上面的计算数据,创建绕x轴旋转矩阵
// 1 0 0 0
// 0 cosα sinα 0
// 0 -sinα cosα 0
// 0 0 0 1
mat4 mx = mat4(1,0,0,0, 0,cos,-sin,0, 0,sin,cos,0, 0,0,0,1);
//引用上面的计算数据,创建绕y轴旋转矩阵
// cosβ 0 sinβ 0
// 0 1 0 0
//-sinβ 0 cosβ 0
// 0 0 0 1
mat4 my = mat4(cos,0,-sin,0, 0,1,0,0, sin,0,cos,0, 0,0,0,1);
//创建绕z轴旋转矩阵
// cosα sinα 0 0
//-sinα cosα 0 0
// 0 0 1 0
// 0 0 0 1
mat4 mz = mat4(cos,-sin,0,0, sin,cos,0,0, 0,0,1,0, 0,0,0,1);
//多个旋转矩阵、顶点齐次坐标连乘 运算从右到左 依次变换
gl_Position = translation*scale*mz*mx*my*apos;
}
</script>
<!-- 片元着色器源码 -->
<script id="fragmentShader" type="x-shader/x-fragment">
void main() {
// 逐片元处理数据,所有片元(像素)设置为红色
gl_FragColor = vec4(1.0,0.0,0.0,1.0);
}
</script>
<script>
//通过getElementById()方法获取canvas画布
var canvas = document.getElementById("webgl");
//通过方法getContext()获取WebGL上下文
var gl = canvas.getContext("webgl");
//顶点着色器源码
var vertexShaderSource =
document.getElementById("vertexShader").innerText;
//片元着色器源码
var fragShaderSource =
document.getElementById("fragmentShader").innerText;
//初始化着色器
var program = initShader(gl, vertexShaderSource, fragShaderSource);
//获取顶点着色器的位置变量apos
var aposLocation = gl.getAttribLocation(program, "apos");
//创建立方体的顶点坐标数据
var data = new Float32Array([
//z为0.5时,xOy平面上的四个点坐标
0.5, 0.5, 0.5, -0.5, 0.5, 0.5, -0.5, -0.5, 0.5, 0.5, -0.5, 0.5,
//z为-0.5时,xOy平面上的四个点坐标
0.5, 0.5, -0.5, -0.5, 0.5, -0.5, -0.5, -0.5, -0.5, 0.5, -0.5, -0.5,
//上面两组坐标分别对应起来组成一一对
0.5, 0.5, 0.5, 0.5, 0.5, -0.5,
-0.5, 0.5, 0.5, -0.5, 0.5, -0.5,
-0.5, -0.5, 0.5, -0.5, -0.5, -0.5,
0.5, -0.5, 0.5, 0.5, -0.5, -0.5,
]);
//创建缓冲区对象
var buffer = gl.createBuffer();
//绑定缓冲区对象
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
//顶点数组data数据传入缓冲区
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
//缓冲区中的数据按照一定的规律传递给位置变量apos
gl.vertexAttribPointer(aposLocation, 3, gl.FLOAT, false, 0, 0);
//允许数据传递
gl.enableVertexAttribArray(aposLocation);
//LINE_LOOP模式绘制前四个点
gl.drawArrays(gl.LINE_LOOP, 0, 4);
//LINE_LOOP模式从第五个点开始绘制四个点
gl.drawArrays(gl.LINE_LOOP, 4, 4);
//LINES模式绘制后8个点
gl.drawArrays(gl.LINES, 8, 8);
//声明初始化着色器函数
function initShader(gl, vertexShaderSource, fragmentShaderSource) {
var vertexShader = gl.createShader(gl.VERTEX_SHADER);
var fragmentShader = gl.createShader(gl.FRAGMENT_SHADER);
gl.shaderSource(vertexShader, vertexShaderSource);
gl.shaderSource(fragmentShader, fragmentShaderSource);
gl.compileShader(vertexShader);
gl.compileShader(fragmentShader);
var program = gl.createProgram();
gl.attachShader(program, vertexShader);
gl.attachShader(program, fragmentShader);
gl.linkProgram(program);
gl.useProgram(program);
return program;
}
</script>
</body>
</html>
默认效果

应用平移矩阵 x y z 分别平移-0.4
mat4 translation = mat4(1,0,0,0, 0,1,0,0, 0,0,1,0, -0.4,0,0,1);
gl_Position = translation*apos; 平移后的效果

应用缩放矩阵 x y z分别缩放0.5
mat4 scale = mat4(0.5,0,0,0, 0,0.5,0,0, 0,0,0.5,0, 0,0,0,1);
gl_Position = scale*apos;缩放后的效果

多重矩阵运算 先缩放后平移
gl_Position = translation*scale*apos; 
应用旋转矩阵 y->x->z 依次分别旋转30度
/设置几何体轴旋转角度为30度,并把角度值转化为弧度值
float radian = radians(30.0);
//求解旋转角度余弦值
float cos = cos(radian);
//求解旋转角度正弦值
float sin = sin(radian);
//引用上面的计算数据,创建绕x轴旋转矩阵
// 1 0 0 0
// 0 cosα sinα 0
// 0 -sinα cosα 0
// 0 0 0 1
mat4 mx = mat4(1,0,0,0, 0,cos,-sin,0, 0,sin,cos,0, 0,0,0,1);
//引用上面的计算数据,创建绕y轴旋转矩阵
// cosβ 0 sinβ 0
// 0 1 0 0
//-sinβ 0 cosβ 0
// 0 0 0 1
mat4 my = mat4(cos,0,-sin,0, 0,1,0,0, sin,0,cos,0, 0,0,0,1);
//创建绕z轴旋转矩阵
// cosα sinα 0 0
//-sinα cosα 0 0
// 0 0 1 0
// 0 0 0 1
mat4 mz = mat4(cos,-sin,0,0, sin,cos,0,0, 0,0,1,0, 0,0,0,1);
//多个旋转矩阵、顶点齐次坐标连乘 运算从右到左 依次变换
gl_Position = mz*mx*my*apos;
应用旋转矩阵后 再缩放在平移 多矩阵结合
多个旋转矩阵、顶点齐次坐标连乘 运算从右到左 依次变换
gl_Position = translation*scale*mz*mx*my*apos;